![]()
Terms of the Music Theory with Audio Samples
| Home | Index | Literature | Documents | Contact |
Modulation is the harmonic transition from one key to another. A simple example is the following modulation from A minor to C major:
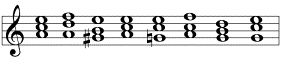
Here, at first, the ear settles into the tone ensemble of A minor, but is then torn out of this key by the tone G. Unless there are any further tones outside of the key of A minor, the perception supposes a key that, firstly, contains the tones that appear together with the tone G, and secondly has maximum accordance with the tone ensemble of the preceding key. That key is, in the above case, C major. A closer examination of the modulation is summarised in the laws of the modulation, which provide the basis for the harmonic analysis of musical pieces.
The modulation implements a harmonic relation between the keys. This relation builds upon the harmony of the tones (consonance) and the harmony of the consonances (tonality) and is thus a harmony of the third dimension: The tone ensembles of different keys harmonise on the basis of their common tones. The usual expression of this kind of harmony is: relationship of the keys.
|
|
|
|
|
The relationship of the keys is based on the accordance of their tone ensembles. The tone ensemble of a key results from its tonal components. During the modulation, a change happens between these tone ensembles and the tonality embodied therein. Thereby, another triad turns into a tonic.
The accordance between two keys is demonstrated in the following using the relation between C major and A minor:
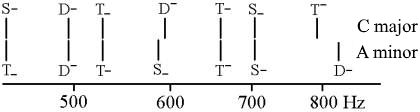
The harmonically in each case differently defined tones (identified by the formulae) coincide in the harmonic comparison of the tonal ensembles if they have nearly or absolutely the same frequency. In the above case, the keys have six common tones, with the tones tuned at 586,67 Hz and 594 Hz (both named D) being considered identical. Their slight difference, which is irrelevant for the differentiation of tones, is referred to as comma in music. The tones having 586,67 Hz and 594 Hz differ by the so-called syntonic comma (81:80).
Considering the two keys above, each one has seven tones, but they form a system of eight tones in which it is possible to modulate back and forth between A minor and C major at any time. If one includes other keys that are more or less related to these keys and to each other, then this results in a closed system of twelve tones, from where no modulation can lead out. The twelve tones of modern music have thus their reason in the principle of the modulation, that is, in the harmonics of the key relationships. On this principle, the system of the 24 keys is based:
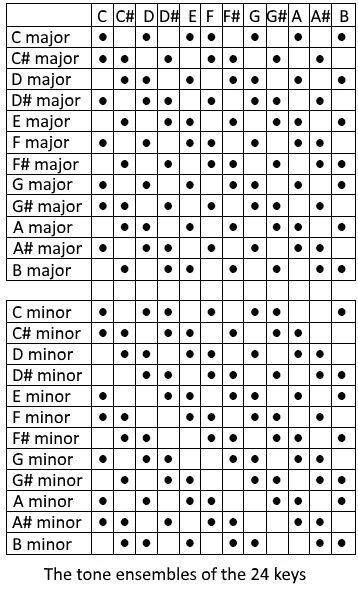
This presentation abstracts – like the perception itself – from the different tunings that a tone can have before and after a modulation. In music, this abstraction is even poured into a uniform and rigid system: the equal temperament.
From the above table, the degree of relatedness of the keys can be seen: the extent of coincidence between the tone ensembles of the keys. This gradation is essential in the case of the modulation because the principle of the maximal accordance is in effect here. In many cases namely, a sound with new tones can occur in various keys. The modulation, however, is always a transition into a harmonically closer related key. If several keys having the same degree of relationship with the preceding key come into question, the sounds remain harmonically uncertain (tonally indifferent) until a uniquely identifiable key is established by further tones. The details are given in the laws of modulation.
|
|
|
|
|
From the concept of the modulation, the following laws can be derived:
1. A key constitutes itself by the occurrence of tones that can only belong exclusively to the tone ensemble of one key.
2. Before the constitution of a key (in the state of the tonal indifference), no modulation (= transition into another key) can take place.
3. A key is exited by the appearance of tones that do not belong to the tone ensemble of this key.
4. A sound by which a key is exited puts a new key into effect if the tone ensemble of this key, firstly, contains the tones of this sound and, secondly, has more tones in common with the tone ensemble of the quitted key than all the other keys in which the tones of this sound can be found (law of the maximum accordance or inertia law of harmonic listening).
5. If a key is exited by a sound that can occur in a number of keys of which none can distinguish itself by a closer relationship to the quitted key, then a tonal indifference occurs.
6. A temporarily occurred tonal indifference can be resolved directly by further sounds, with the help of which a new key can be identified according to the law of maximum tonal agreement.
7. A temporarily occurred tonal indifference can be resolved indirectly by a sound which retrospectively presents to the perception a sequence of two modulations that have a maximum tonal accordance as a whole.
8. A tonal indifference can be prolonged by further indifferent sounds that could belong to a changing spectrum of keys so that the harmonic connection to the quitted key is lost (for example: a semitone-wise shifted [= chromatic] sequence of diminished seventh chords).
9. If a key is exited by a sound that cannot occur in any key, then the harmonic context with the quitted key is lost by this atonal sound.
10. The lost context with a quitted key excludes any modulation at first and requires the renewed constitution of a key (see point 1).
The derivation of these laws from the principle of modulation as well as the more precise representation using examples of notes can be found in the 3rd chapter of the book "Tonal Music".
|
|
|
|
|
The term 'secondary dominant' is based on a misconception: Under this title, the dominant of a new key is erroneously regarded as a chord that still belongs to the preceding key. Each definition of the secondary dominant denies explicitly that the key has been changed, although, at the same time, it is taken note of the fact that the tones of this chord do not occur in the previous key. This category is, insofar, one of the constructs of the altered chord, where the key is in principle considered separately from the tones of which it consists.
|
|
|
|
|
A special constellation of a modulation in which the last sound of the previous key is a distinctive dissonance (that is to say: no pseudo consonance) and the first sound of the new key is a tonic. In this case, the dissonance appears in need for resolution as long as it sounds. However, its need for resolution becomes superfluous by the change into the new key. On the other hand, the tonic of the new key – like every tonic – does not require a resolution. Therefore it seems as if the tonic of the new key were the resolution of the preceding dissonance.
In the following example, the tonic of G major seems to be the resolution of a dissonance that cannot belong to the key of G major:

The pseudo resolution feeds the impression that the seemingly resolved dissonance belongs to the tonic of the new key. The music theory has elaborated this impression to the illusion that even "non-scale" tones belong to a key, that is, even such tones that have, because of the harmonics of the tonality, nothing to do with the tone ensemble of this key. This error, however, is especially based on the confusion of the modulation with the shape that this harmonic transition assumes at the level of the melodic: the alteration. This error lives a life of its own by the construct of the altered chord.
|
|
|
|
|
Tonal analysis of a piece of music
The following analysis (created by a computer program) shows, below the stave, the keys which can be identified in the harmony sequence on the basis of the laws of the modulation. If the key is known, the tones belonging to the tonic, dominant, and subdominant are also known. This is why the tonal composition of the sounds can be given above by a harmonic formula.
J. S. Bach, The Well-Tempered Clavier I, Prelude I, BWV 846 (simplified)

- Bar 1-2: Indifference according to the 1. law, because F major would also be possible.
- Bar 3: Constitution of the key of C major according to the 1. law.
- Bar 6: Modulation according to the 4. low. The same applies to almost all further modulations.
- Bar 14: Tonal indifference according to the 5. law.
- Bar 15: Indirect resolution of this indifference according to the 7. law: Modulations to A minor and then to C major are harmonically nearest. The notation of the G sharp in the key of A minor as A flat is a writing-technically motivated enharmonic change, of which this prelude contains further examples.
- Bar 23-25: Example for a pseudo resolution
|
|
|
|
|
Virtually imperceptible difference between two tone pitches; strictly speaking: the frequency ratio between two different tunings of one and the same tone; because a harmonically distinctive tone relation is first perceived in the range of a semitone. From the standpoint of the just intonation, commas occur in the case of modulations when the coinciding tones of different keys do not have the same frequency. The most frequent comma is the syntonic comma with the frequency ratio 81:80. It occurs, for example, between the dissonant minor third (32:27) and the consonant minor third (6:5). Because:
(6:5) x (27:32) = 81:80
An example: The tones D and F form in the key of A minor the minor third of the subdominant (6:5), but after the transition to C major a pseudo consonance (32:27), which results from the relation between the subdominant root tone and dominant fifth, which lies three fifths further away. This relation exists in a dyad with the formula
![]()
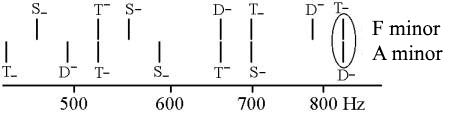
However, the syntonic comma is not the only comma in music. The largest one has the frequency ratio 128:125 and occurs, for example, in a (purely intonated) modulation from A minor to F minor:
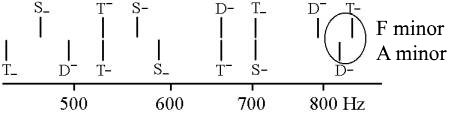
The two lines within the circle show the difference between the two tunings of the same tone. This comma disappears with the equal temperament because of an even detuning of the tones:
|
|
|
|
|
Exact pitch of a tone in the spectrum of the possible fluctuations (commas). From the standpoint of the just intonation, the pitch of individual tones is variable because of the modulation. The capability of the perception to abstract from these fluctuations of the musical tuning allows for a uniform and inflexible tuning of the tones by the temperament.
|
|
|
|
|
Exact frequency ratios within the tone ensemble of a key on the basis of the tonality and its consonant components (3:2, 5:4, 6:5). Since the tuning of the tones can change because of the modulation, the temperament has become usual as an inflexible tuning of the instruments. The just intonation has therefore almost only a theoretical importance because it underlies the temperament and is necessary for its explanation.
|
|
|
|
|
During the historic transition to the tonal music, the problem arose for instruments with fixed tones that the just intonation required a limitation to a particular key because individual tunings of the tones can change after a modulation and therefore be different (the difference is named comma). Therefore, various tempered scales have been created in order to compensate for the differences of the tunings in the case of modulations. For a long time, the mean-tone tuning was considered to be optimal because it came as close as possible to the just intonation (especially in the case of the thirds). But it had the downside that it limited the music played to the range of a few keys and led to cacophonous 'wolf intervals'. Regarding their detunings, these intervals exceed the dimension of the comma and approximate the range of the perceptible tone relation, that is, that of the semitone.
The best possible solution of this problem has been achieved by the equal temperament, for which a larger detuning of the thirds within a key has been accepted in order to overcome all limitations of the modulation. In this tuning, the octave (2:1) is divided into 12 equal tone relations, which therefore have the frequency ratio 21/12:1. In this tuning, all keys sound equally acceptable. The tones that are perceived as identical in the course of a modulation are thereby presented also in an acoustically uniform manner.
|
Consonance |
Just intonation |
Equal temperament |
Detuning ratio |
|
Fifth |
3:2 = 1,5000 |
27/12 = 1,4983 |
1,0011 |
|
Major third |
5:4 = 1,2500 |
25/12 = 1,2599 |
1,0079 |
For a comparison between the just intonation and the equal temperament see also: comma.
|
|
|
|
|
| © 2020 Franz Sauter, Hamburg | Data Protection |